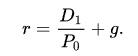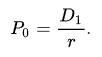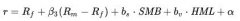DDM_股息貼現(xiàn)模型
2024-06-28 17:15
來源:未知
作者: admin
在線咨詢:
-

掃描或點(diǎn)擊關(guān)注格雷厄姆網(wǎng)在線客服
股息貼現(xiàn)模型縮寫:DDM,是現(xiàn)金流折現(xiàn)模型的一種特殊形式,僅用于為公司的股權(quán)資產(chǎn)定價。其用于以投資者角度估算公司股票價格的合理值,原理就是把預(yù)期將來派發(fā)的一系列股息按利率貼現(xiàn)成現(xiàn)值,一系列股息的凈現(xiàn)值的總和相加即為該股票的合理價值。這條方程又可稱為戈登增長模型。以學(xué)者邁倫·J.戈登命名,因?yàn)閷W(xué)術(shù)界傳統(tǒng)認(rèn)為戈登在1959年首先提出這模型,但實(shí)際上其理論基礎(chǔ)可追溯至1938年由經(jīng)濟(jì)學(xué)家約翰·伯爾·威廉姆斯發(fā)表的文章《投資價值理論》。
一般來說,股息貼現(xiàn)模型的公式可以表述如下:
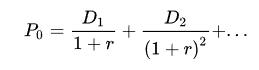
其中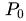 代表某一企業(yè)股權(quán)的現(xiàn)值(當(dāng)前股票價格)、
代表某一企業(yè)股權(quán)的現(xiàn)值(當(dāng)前股票價格)、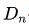 代表當(dāng)前預(yù)測的未來第n期發(fā)放的股息、
代表當(dāng)前預(yù)測的未來第n期發(fā)放的股息、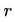 代表股息的貼現(xiàn)率,即權(quán)益成本(對投資者來說,是他的期望回報率)。
代表股息的貼現(xiàn)率,即權(quán)益成本(對投資者來說,是他的期望回報率)。
由于未來的股息有不確定性,故公式可改寫為:
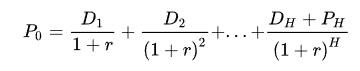
H代表持有股票的時間長度,這式能強(qiáng)調(diào)投資股票不僅旨在收取股息,還能說明股票價格上升所帶來的資本增殖亦是投資的另一目的。
原始折算現(xiàn)金流的股息貼現(xiàn)模型需要對未來無限期的股息進(jìn)行預(yù)測,而這肯定是不可能的事[2]。因此,如果期望每年股息維持相同百分比增加,股息貼現(xiàn)模型可改寫成以下形式:
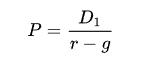
同樣地, P是股價的現(xiàn)值、g是股息的期望永久增長率、r是公司的權(quán)益成本,從投資者角度來說就是他的期望回報率。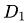 是下年度的股息(已知值,非期望值)。當(dāng)公司管理層公布下年度的股息時,不應(yīng)該采用現(xiàn)行股息和增長率來計算其股價。
是下年度的股息(已知值,非期望值)。當(dāng)公司管理層公布下年度的股息時,不應(yīng)該采用現(xiàn)行股息和增長率來計算其股價。
這一模型的涵義是:股東從公司獲得的收入的根本來源是股息,所以股東權(quán)益的當(dāng)前價值等于其未來所獲得的股權(quán)的現(xiàn)值之和。
假設(shè)
股息以固定百分比增加。
固定的增長會無限維持。
公司的權(quán)益成本(r)必須大于增長率(g),否則模型由于分母為負(fù)數(shù)而變得無意義。
等式的推導(dǎo)
模型把無窮級數(shù)相加,從而得出股票現(xiàn)行價格,P。通俗來說,股息的增長率在本模型中可被假定為永久保持不變,從而股息是按同一比例逐年增加。
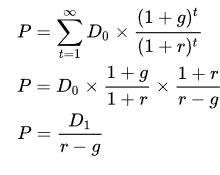
另一種推導(dǎo)方法
投資者的投資期內(nèi)總回報(Total Return)可分成兩部分:一部分是投資者獲得的股息收入(Income),另一部分則是股價上升帶來的回報,即是資本的增殖(Capital Gain)。以文字表達(dá)算式如下:
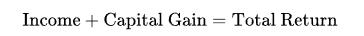
等式上的三個部分同時除以現(xiàn)時股票價格,于是三部分轉(zhuǎn)為:
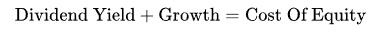
把文字表達(dá)式轉(zhuǎn)回代數(shù)式:

再把所有代數(shù)位置稍微調(diào)整:
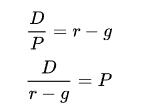
這推導(dǎo)辦法把股價的增長率作為股息增長率的近似數(shù),也把公司的資本成本作為投資者期望總回報的近似數(shù),這推導(dǎo)算式才得以成立。要把公司的資本成本當(dāng)作投資者期望回報的近似值,唯一的假設(shè)是此公司完全是股權(quán)融資,不存在任何借貸或債券融資。至于股價的增長近似于股息的增長,則因?yàn)榇四P桶凳竟蓛r的增來自于未來股息以現(xiàn)金流角色所帶來的股票價格凈現(xiàn)值增加,因此股價的增長率和股息的增長率只有微小的差異。
股息增長率與權(quán)益成本的關(guān)系
正如假設(shè)所指出,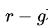 不應(yīng)該是負(fù)數(shù),換言之股息的增長率不能超越權(quán)益成本。但是,某些時候公司可能派發(fā)大額的特別股息(例如公司大規(guī)模出售資產(chǎn)、大股東操控管理層玩弄財技得到大筆現(xiàn)金等),股息增長率可能短期內(nèi)大幅度上升,這時候股息貼現(xiàn)模型可修改為兩階段的股息增長模型,這樣在不違反模型的假設(shè)下,可使模型適應(yīng)這些特殊情況評估股票價值。二階段模型的前半部分表示股息快速增長,后半部分是表示股息水平回復(fù)固定的增長率:
不應(yīng)該是負(fù)數(shù),換言之股息的增長率不能超越權(quán)益成本。但是,某些時候公司可能派發(fā)大額的特別股息(例如公司大規(guī)模出售資產(chǎn)、大股東操控管理層玩弄財技得到大筆現(xiàn)金等),股息增長率可能短期內(nèi)大幅度上升,這時候股息貼現(xiàn)模型可修改為兩階段的股息增長模型,這樣在不違反模型的假設(shè)下,可使模型適應(yīng)這些特殊情況評估股票價值。二階段模型的前半部分表示股息快速增長,后半部分是表示股息水平回復(fù)固定的增長率:
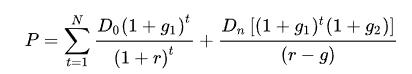
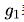 表示短期內(nèi)表現(xiàn)超然的期望增長率、
表示短期內(nèi)表現(xiàn)超然的期望增長率、 表示回復(fù)固定的增長率、 t代表短期增長率出現(xiàn)的時間長度。
表示回復(fù)固定的增長率、 t代表短期增長率出現(xiàn)的時間長度。
同理,模型也可加入股息增長率遞減的情況,求出三階段的股息增長模型:
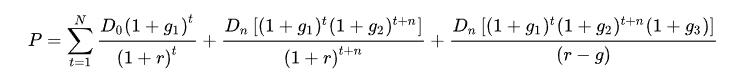
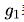 表示短期內(nèi)表現(xiàn)超然的期望增長率、
表示短期內(nèi)表現(xiàn)超然的期望增長率、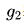 表示后續(xù)另一短期股息呈現(xiàn)下降的增長率、n代表該后續(xù)短期、
表示后續(xù)另一短期股息呈現(xiàn)下降的增長率、n代表該后續(xù)短期、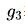 表示回復(fù)固定的增長率、t代表短期增長率出現(xiàn)的時間長度。
表示回復(fù)固定的增長率、t代表短期增長率出現(xiàn)的時間長度。
另外,透過計算 r,等式可逆向計算公司的資本成本。
模型的缺陷
如前所述,股息貼現(xiàn)模型產(chǎn)生于1938年,由美國經(jīng)濟(jì)學(xué)家約翰·伯爾·威廉姆斯最早提出。當(dāng)時投資者買進(jìn)股票的主要目的確實(shí)是獲得股息,股票的股息率經(jīng)常被用來和債券的孳息率做對比。但是,自從20世紀(jì)中期以后,由于稅收上的考慮,上市公司逐漸減少了股息的發(fā)放,轉(zhuǎn)而傾向于保留大部分收益用作再投資,以避免股東繳納高昂的股息稅。當(dāng)公司需要把一部分資金分配給股東的時候,往往采取股票回購的方式,而非發(fā)放股息。這種情況是股息貼現(xiàn)模型無法應(yīng)對的。
除此之外,模型本身的假設(shè)也存在技術(shù)上問題:
股息率問題:現(xiàn)實(shí)中穩(wěn)定而且永久維持的普通股股息增長率未曾存在,這假設(shè)明顯失真,業(yè)績高增長的公司幾乎不派發(fā)股息[6],從而導(dǎo)致模型的簡化版本不適用,但按逐期現(xiàn)金流貼現(xiàn)的模型形式(即上方第一條公式)依然有效。
派息問題:未必所有普通股股票均會派息,因?yàn)榕上䦟?dǎo)致股價短期下降,而且公司管理層可能更傾向于股息資本化,即不派發(fā)股息而為公司保留現(xiàn)金作投資(會計學(xué)稱之為留存收益)。假若沒有股息,股東沒有現(xiàn)金流的增加,他所持有的股票現(xiàn)值也不會有所增長。因此,更常見的辦法是借用莫迪尼亞尼-米勒定理,假定股息派發(fā)與否對公司價值沒有影響,從而在模型中以每股溢利取代股息作為參數(shù)。但是,溢利增長率又不同于股息增長率,兩者的計算結(jié)果可能有別。
模型中,股價對股息增長率的變化非常敏感,而股息增長率只是一個期望數(shù)據(jù)。
投資者預(yù)期問題:如果投資者沒有預(yù)期收取股息,模型便意味著股票沒有任何價值[2]。因此,必須假設(shè)投資者預(yù)期會收到現(xiàn)金。
但是,由于優(yōu)先股的股息是固定且必須派發(fā)的,再者優(yōu)先股亦無到期日,其回報形式類似于永久年金或者債券,因此股息貼現(xiàn)模型可適用于評估優(yōu)先股的價值[7]。因?yàn)閮?yōu)先股股息數(shù)額固定,換言之g等于0,未來股息總和的現(xiàn)值就相當(dāng)于股價,其計算公式即是:
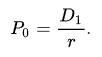
本文由東方銅牛網(wǎng)整理編輯,轉(zhuǎn)載 DDM_股息貼現(xiàn)模型 請注明文章地址鏈接。
廣告
熱門搜索
相關(guān)文章
廣告
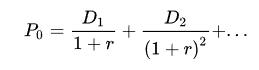
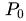 代表某一企業(yè)股權(quán)的現(xiàn)值(當(dāng)前股票價格)、
代表某一企業(yè)股權(quán)的現(xiàn)值(當(dāng)前股票價格)、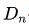 代表當(dāng)前預(yù)測的未來第n期發(fā)放的股息、
代表當(dāng)前預(yù)測的未來第n期發(fā)放的股息、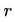 代表股息的貼現(xiàn)率,即權(quán)益成本(對投資者來說,是他的期望回報率)。
代表股息的貼現(xiàn)率,即權(quán)益成本(對投資者來說,是他的期望回報率)。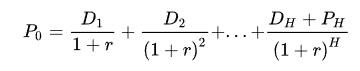
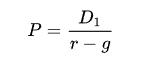
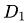 是下年度的股息(已知值,非期望值)。當(dāng)公司管理層公布下年度的股息時,不應(yīng)該采用現(xiàn)行股息和增長率來計算其股價。
是下年度的股息(已知值,非期望值)。當(dāng)公司管理層公布下年度的股息時,不應(yīng)該采用現(xiàn)行股息和增長率來計算其股價。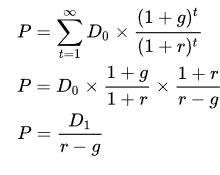
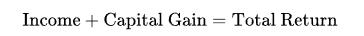
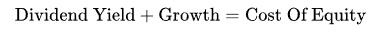

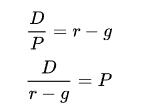
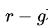 不應(yīng)該是負(fù)數(shù),換言之股息的增長率不能超越權(quán)益成本。但是,某些時候公司可能派發(fā)大額的特別股息(例如公司大規(guī)模出售資產(chǎn)、大股東操控管理層玩弄財技得到大筆現(xiàn)金等),股息增長率可能短期內(nèi)大幅度上升,這時候股息貼現(xiàn)模型可修改為兩階段的股息增長模型,這樣在不違反模型的假設(shè)下,可使模型適應(yīng)這些特殊情況評估股票價值。二階段模型的前半部分表示股息快速增長,后半部分是表示股息水平回復(fù)固定的增長率:
不應(yīng)該是負(fù)數(shù),換言之股息的增長率不能超越權(quán)益成本。但是,某些時候公司可能派發(fā)大額的特別股息(例如公司大規(guī)模出售資產(chǎn)、大股東操控管理層玩弄財技得到大筆現(xiàn)金等),股息增長率可能短期內(nèi)大幅度上升,這時候股息貼現(xiàn)模型可修改為兩階段的股息增長模型,這樣在不違反模型的假設(shè)下,可使模型適應(yīng)這些特殊情況評估股票價值。二階段模型的前半部分表示股息快速增長,后半部分是表示股息水平回復(fù)固定的增長率: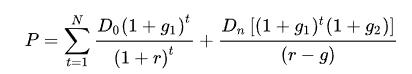
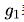 表示短期內(nèi)表現(xiàn)超然的期望增長率、
表示短期內(nèi)表現(xiàn)超然的期望增長率、 表示回復(fù)固定的增長率、 t代表短期增長率出現(xiàn)的時間長度。
表示回復(fù)固定的增長率、 t代表短期增長率出現(xiàn)的時間長度。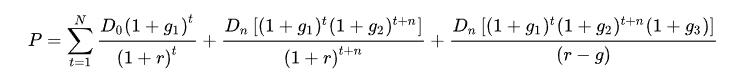
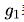 表示短期內(nèi)表現(xiàn)超然的期望增長率、
表示短期內(nèi)表現(xiàn)超然的期望增長率、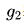 表示后續(xù)另一短期股息呈現(xiàn)下降的增長率、n代表該后續(xù)短期、
表示后續(xù)另一短期股息呈現(xiàn)下降的增長率、n代表該后續(xù)短期、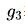 表示回復(fù)固定的增長率、t代表短期增長率出現(xiàn)的時間長度。
表示回復(fù)固定的增長率、t代表短期增長率出現(xiàn)的時間長度。